摘要: 基于混凝土干濕循環試驗和混凝土細觀力學對混凝土在海水侵蝕環境下力學性能的變化進行了研究。混凝土干濕循環試驗方面,采用加速腐蝕試驗,對混凝土試件和根據混凝土配比制成的砂漿試件進行0次、10次、20次、30次、40次和50次干濕循環,利用大型混凝土靜、動三軸試驗系統,檢測了海水侵蝕作用對混凝土抗壓強度、抗拉強度、彈性模量及應力- 應變關系的影響。基于混凝土細觀力學理論,對混凝土試塊進行了細觀數值模擬,考慮了混凝土各組成相的非均勻性,各組成相的材料性質按照Weibull分布來賦值,同時為反映海水侵蝕作用對混凝土的影響,砂漿的強度和彈性模量均以砂漿干濕循環試驗所得結果為準。建立了混凝土隨干濕循環次數變化的抗壓強度折減模型:F=53.789e-0.0117N,抗拉強度折減模型:F=5.3794e-0.01N和彈性模量的折減模型:E=64.735e-0.0191N。
關鍵詞:混凝土;抗侵蝕性;人工海水;細觀數值模擬;加速腐蝕試驗;
0. 引言
眾所周知,混凝土在海洋與沿海、道路除凍鹽、鹽堿地、工業鹽環境中會發生侵蝕破壞,這種破壞的主要原因是混凝土遭受環境中氯離子、鎂離子和硫酸根的侵蝕,這些有害離子通過混凝土孔隙進入到內部,并與混凝土中的氫氧化鈣及水化鋁酸鈣作用生成新的鹽類物質,生成的難溶鹽類物質往往產生較大的體積膨脹,在孔隙的內部產生很大的內應力,長期的積累會使混凝土開裂;一些可溶性的鹽在海水的反復沖刷下溶解析出,使混凝土孔隙率增加,增大了氯離子滲入混凝土內部的孔道,加劇了鋼筋銹蝕,并使混凝土漲裂剝落。另外,如果水灰比控制不嚴,施工質量較差,混凝土振搗不密實,甚至出現蜂窩麻面等現象,這些都會加劇鹽溶液環境對混凝土的侵蝕,使結構變得松軟,強度降低,耐久性下降[2]。
目前,關于混凝土經海水侵蝕作用后力學性能變化的研究較少,而基于混凝土細觀力學對混凝土在海水侵蝕作用后的數值分析的研究還未見相關報道。文獻[2-4]通過加速腐蝕試驗研究了普通硅酸鹽水泥和礦渣硅酸鹽水泥在海水侵蝕后物理力學性能的變化,但沒有進行混凝土細觀力學方面的分析。文獻[6]分析了不同界面參數、不同砂漿損傷參數、不同加載形式對混凝土試件的變形特點、破壞形式以及承載能力的影響,探討了混凝土宏觀力學性能(如應變軟化和剪脹等性質)的細觀機制。文獻[7]研究了主要力學參數的隨機分布對混凝土試件宏觀表征力學性質的影響。以上研究均沒有將試驗和數值分析結合起來,也沒有通過細觀數值分析研究混凝土受海水侵蝕的影響。
本文通過將混凝土干濕循環試驗和細觀力學分析相結合,建立了海水侵蝕作用下混凝土力學性能退化模型,對混凝土受海水侵蝕作用影響的研究方面具有一定的參考價值。
1. 混凝土干濕循環試驗
進行干濕循環試驗的混凝土試件規格為100mm×100mm×100mm。 試件均采用標準鋼模成型,24h拆模后露天蓋草袋養護。表1為每立方米混凝土的配合比及性能指標。
為了在短時間內進行有效的試驗,本試驗采用人工海水作為侵蝕液,配制5倍于海水濃度的侵蝕液,稱為人工海水。人工海水中各種鹽含量見表2。


混凝土力學性能試驗,是在大型三軸電液伺服試驗機上完成的。試驗時,將試件安裝在試驗機的加載板間,試件加載面與加載板之間采取減摩措施,減摩材料采用塑料薄膜和甘油。每種工況至少試驗3個試件,當發現離散較大時,增加試件數目,以求數據的完整準確, 試件承受的壓力、位移和應變值均由計算機動態采集。
1.1試塊單軸劈裂抗拉試驗
混凝土立方體劈裂抗拉強度按下式計算:

混凝土隨不同干濕循環次數變化的抗拉強度的試驗結果如表3所示,混凝土的破壞情況如圖1所示。

本試驗采用實驗室加速試驗方法,即按不同水灰比制備100mm×100mm×100mm的混凝土試件,將成型試件在標準養護室中養護28天。到56天齡期開始浸—烘循環。為了減少試驗結果的離散性,分別將循環試件全部浸泡在人工海水溶液中16小時,然后拿出置于80℃條件下烘8小時為一個循環,如此反復循環,在此期間每間隔10次分別測定試件的抗壓和抗拉強度。
1.2試塊單軸壓縮試驗
實驗所得混凝土在單軸壓縮載荷作用下隨不同干濕循環次數變化的應力-應變曲線的試驗結果如圖2所示,混凝土單軸受壓后破壞情況如圖3所示。

2. 混凝土細觀力學分析
2.1混凝土數值模型
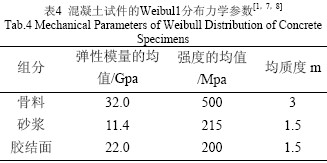
基于混凝土細觀力學,利用RFPA 數值模擬軟件,把混凝土視為由砂漿基質骨料以及兩相之間界面組成的三相復合材料。為了考慮各組成相的非均勻性,各組成相的材料性質按照Weibull 分布來賦值。首先,用一個Weibull 分布來表達整個試樣的材料性質分布, 這相當于生成砂漿基質試樣,該試樣的力學性質要與真實的硬化水泥砂漿體的參數基本一致。然后,在該基質試樣中添加骨料顆粒,程序會自動搜索骨料的邊界并把邊界上的單元賦上相應的力學參數。骨料的參數參照巖石的力學性質參數選取,對于普通混凝土,骨料的強度相對于砂漿基質的強度較高,并且其均值度也較高。砂漿的參數參照依據混凝土配比制成的砂漿試件的干濕循環試驗所得到的結果進行賦值。界面的參數沒有現成的試驗依據,參數取值參考文獻[1]。
為了反映海水侵蝕作用對混凝土性能的影響,根據混凝土的配比制成了砂漿試件并對其進行了10次、20次、30次、40次和50次的干濕循環試驗,在干濕循環后分別進行了劈裂抗拉試驗和單軸壓縮試驗測得了其抗拉強度、抗壓強度和彈模。利用式(2)和式(3)得到了數值模擬時砂漿基質在Weibull分布賦值時的彈性模量和強度的均值,見表5。


2.2細觀單元的彈性損傷本構關系
一般認為,混凝土應力-應變曲線的非線性是由于其受力后的不斷損傷所引起的微裂紋萌生和擴展造成的,而不是由于其塑性變形引起。因次,用彈性損傷力學的本構關系來描述混凝土的細觀單元的力學性質是合適的。按照應變等價原理,認為應力σ 作用在受損材料上引起的應變與有效應力作用在無損材料上引起的應變等價。根據這一原理,受損材料的本構關系可通過無損材料中的名義應力得到,即
σ =Eo(1−D)ε (4)
式中:Eo為初始彈性模量;D 為損傷變量。
2.2.1拉伸損傷演化方程
單軸拉伸應力狀態下,細觀單元的彈性損傷本構關系如圖4所示。相應地,損傷的定量表達式為(5)。

式中: ftr是單元的殘余強度;εto是彈性極限所對應的拉伸應變,該應變可以叫做拉伸損傷應變閾值;εtu是單元的極限拉伸應變,當單元單軸拉伸應變達到極限拉伸應變時,單元將完全損傷,達到拉伸斷裂(破壞)狀態,即D =1。
2.2.2壓縮剪切損傷演化方程
為了反映細觀單元在壓縮或剪切應力下的損傷,這里選擇摩爾庫倫準則作為第二個損傷閾值判據。

抗壓強度(為正數);σ1和σ3分別為細觀單元的最大和最小住應力值。

式中:εco為單元應力達到抗壓強度時的壓應變;εcu為極限壓應變,取定值為0.0033。當應變達到極限壓應變時,單元的剛度將急劇退化為接近于0 矩陣的矩陣[9]。
2.3數值模擬
建立100mm×100mm混凝土試件的隨機骨料(斷面骨料填充率為40;骨料的粒徑范圍為5~20mm,規格比例為:5~10:10~20=30:70)細觀數值模型,并把它剖分為0.5mm×0.5mm的有限元網格。
2.3.1拉伸損傷破壞
混凝土在劈拉載荷作用下隨不同干濕循環次數變化的抗拉強度的數值模擬結果如表6所示,混凝土破壞情況如圖6所示。

2.3.2壓縮損傷破壞
混凝土在單軸壓縮載荷作用下隨不同干濕循環次數變化的應力-應變曲線的數值模擬結果如圖7所示,混凝土單軸受壓后破壞情況如圖8所示。


通過表3 與表6 混凝土抗拉強度試驗值與計算值的對比,圖1 與圖6 混凝土單軸壓縮應力-應變關系曲線的對比以及圖1、3 與圖6、8 裂紋產生、發展和貫通情況的對比可以發現基于混凝土細觀力學進行數值模擬的計算結果與混凝土干濕循環試驗所得的試驗結果吻合較好。
3. 混凝土在海水侵蝕作用后的力學性能退化模型
通過以上混凝土干濕循環試驗和混凝土細觀力學分析,將得到的混凝土在不同干濕循環次數下的極限抗壓強度、極限抗拉強度和彈性模量的試驗結果和計算結果進行了整合,利用計算結果和試驗結果的互補性,得到了混凝土隨干濕循環次數變化的抗拉強度折減曲線、抗壓強度折減曲線和彈性模量折減曲線以及相應的的折減方程。
通過最小二乘法得到的混凝土隨干濕循環次數變化的抗拉強度折減方程(8)及相應的抗拉強度折減曲線如圖8:
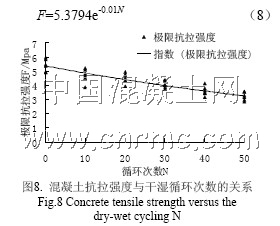
通過最小二乘法得到的混凝土隨干濕循環次數變化的抗壓強度折減方程(9)及相應的抗壓強度折減曲線如圖9:

通過最小二乘法得到的混凝土隨干濕循環次數變化的彈性模量折減方程:
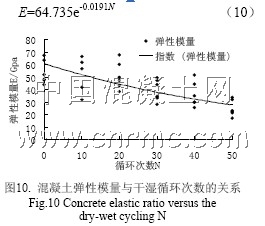
4. 結 論
通過本文的試驗研究和細觀力學分析,可以得到以下結論:
(1)混凝土在單軸壓荷載作用下的極限拉應力、極限壓應力和彈性模量隨干濕循環次數的增加逐漸降低,50次干濕循環以后抗拉強度降低約40.4%,抗壓強度降低約33.4%,彈性模量降低約60.8%;
(2)由數值模擬得到的虛擬試驗結果與真實結果的誤差在允許范圍內,而且由模擬單軸抗拉、抗壓所得到的混凝土的開裂位置、開裂方向和應力-應變曲線等情況均與試驗結果吻合較好;
(3)根據試驗結果和計算結果,建立了混凝土隨干濕循環次數變化的抗壓強度折減模型:
F=53.789e-0.0117N,抗拉強度折減模型:F=5.3794e-0.01N和彈性模量的折減模型:E=64.735e-0.0191N;
(4)本文著重從混凝土細觀力學的角度研究海水侵蝕作用對混凝土力學性能的影響,通過與試驗結果的比較可知,該種方法對混凝土受海水侵蝕作用的模擬結果與試驗結果較為吻合,對混凝土受海水侵蝕作用影響的研究方面具有一定的參考價值;
參考文獻
[1] 唐春安,朱萬成.混凝土損傷與斷裂—數值試驗[M].北京:科學出版社,2003
[2] ZHANG Y M,WANG TC. Prediction for Seawater-cor-rosive concrete strength
by BP neural network[J] .Jour-nal of Jinan University,2003, (3):248-250 .
[3] 張玉敏,王鐵成.人工海水對混凝土侵蝕性的研究[J].混凝土.2001,11:48-50.
[4] 張玉敏,王鐵成.人工海水對混凝土侵蝕性的研究(續)[J]. 混凝土.2001,12:51-53.
[5] Harvey H. Haynes. Permeability of Concrete in Sea Water [J]. Special
Publication.2004,(65):1-38.
[6] KANG J F. The basic problems on the research of concrere in the environment with sulphate [J]. Concreat.1995, (3):9-18.
[7] 夏曉舟,章青,湯書軍.混凝土細觀損傷破壞過程的數值模擬[J].河海大學學報(自然科學版),2007,35(3):319—325.
[8] 李建波,林皋,陳健云.混凝土損傷演化的隨機力學參數細觀數值影響分析[J].建筑科學與工程學報,2004,24(3):7—12.
[9] 林皋,李建波,趙娟,梁正召.單軸拉壓狀態下混凝土破壞的細觀數值演化分析[J].建筑科學與工程學報.2007,24(1):1—6.
[10] Werner Riedel, Markus Wicklein, Klaus Thoma. Shock properties of
conventional and high strength concrete Experimental and mesomechanical
analysis[J].International ournal of Impact Engineering.2008,35(3):155-171.
[11] L.T. Moa,b,, M. Huurmana, S.P.Wub, A.A.A. Molenaara.2D and 3D
meso-scale finite element models for ravelling analysis of porous asphalt
concrete[J].Finite Elements in Analysis and Design. 2008,44(4):186-196.
[12]過鎮海.混凝土的強度和變形-試驗基礎和本構關系[M].北京:清華大學出版社,1997.

















