摘要:收集了158 根集中荷載作用下高強混凝土無腹筋梁的抗剪試驗數據,將抗剪強度試驗結果與中國規范(GB50010-2002)和ACI 規范(ACI318-2002)理論計算結果相比較,并分析了混凝土強度、剪跨比、截面尺寸和縱筋配筋率對梁抗剪強度的影響。結果表明:中國規范公式對小剪跨比梁偏于保守,對大剪跨比梁不夠安全;ACI 公式高估了混凝土強度的影響,低估了剪跨比的影響,計算結果偏于保守;兩公式均沒有合理考慮甚至忽視了尺寸效應和縱筋配筋率對梁抗剪強度的影響。
關鍵詞:高強混凝土;無腹筋梁;抗剪強度
1 引言
梁斜截面抗剪承載力問題是混凝土結構基本理論中的經典問題之一。因其破壞機理復雜,影響因素眾多一直備受國內外學者關注。近一百年來,國內外對混凝土梁在不同荷載作用情況下的抗剪性能進行了大量的試驗研究,采用了非常精巧的分析工具,但是仍然沒有完全弄清楚。各國規范提供的抗剪承載力計算公式,大多是通過對大量的實驗結果的分析,同時采用數理統計方法建立起來的。
美國混凝土協會提出圓柱體抗壓強度設計值大于41Mpa 的混凝土為高強混凝土,我國根據當前的設計和施工水平,認為混凝土強度等級大于C50 的混凝土為高強混凝土[1]。隨著經濟水平的不斷提高,高強混凝土在工程中的應用越來越普遍。由于高強混凝土水泥用量大,流動性較大,與普通混凝土相比,脆性增加,性能上也有所不同。現行規范公式用于高強混凝土無腹筋梁抗剪強度計算,對抗剪強度各主要影響因素的評估是否仍然合適,會否造成計算的安全度降低,是有待研究解決的問題。
2 高強混凝土無腹筋梁抗剪試驗概況
本文收集了從上個世紀八十年代以來,國內外研究者進行的高強混凝土無腹筋梁在集中荷載作用下抗剪承載力試驗的數據共158 個,列于表1 中。從表中可見,國外研究者的試驗數據較多,國內只收集到清華大學[2][7]和重慶大學[12]的試驗數據。所列數據的高強混凝土梁均為矩形截面,試驗變化的參數主要為梁的混凝土強度等級,剪跨比和縱筋配筋率。所有試驗數據中混凝土強度等級均在C50 至C120 之間,剪跨比在1~7 之間,縱筋配筋率在1.2~6.6 之間。Kim[8]的試驗除了考慮以上三種因素以外,還探討了截面有效高度對梁抗剪強度的影響。

3 試驗值與計算值的比較分析
對收集到的試驗數據,分別根據我國規范GB50010-2002 抗剪公式(1)和ACI 318-2002抗剪公式(2)進行抗剪強度的計算。將試驗值與計算結果的比較列于表2,可見vtest/vChina的均值為1.4,離散系數為0.512;而vtest/vACI的均值為2.68,離散系數為0.715。表明對于高強混凝土無腹筋梁的抗剪強度計算,ACI 規范安全度較高,但是偏于保守,中國規范的試驗結果符合情況相對較好,但是安全度有所降低。
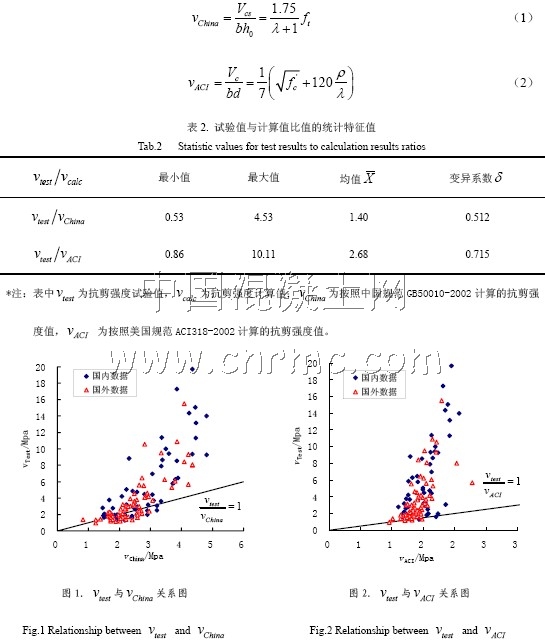
圖1給出中國規范公式計算值與抗剪強度試驗值的散點圖,圖中顯示對試驗抗剪強度vtest≤3.5Mpa 的梁,有相當一部分點落在了vtest/vChina=1以下;而當vtest >6Mpa 時,試驗值又遠遠大于計算值。進一步研究發現抗剪強度vtest/vChina<1的數據共有41 組,除少數為剪跨比為2 以外,均為剪跨比λ > 3的梁;而vtest>6Mpa 的試驗數據共有27 組,除4 組為剪跨比λ = 2 的梁,其余均為λ =1~1.5的梁。由此可見,中國規范公式用于高強混凝土無腹筋梁時,對于小剪跨比的梁偏于保守,對于大剪跨比的梁則不夠安全。圖2 給出ACI 公式計算值與試驗值的散點圖,圖中除了5 個點試驗值小于計算值以外,其余的試驗值均大于計算值,部分數據遠遠高于計算結果。進一步研究表明vtest/vACI<1的5 根梁均為剪跨比λ > 3的梁,試驗值遠遠高于計算值的梁多為剪跨比較小的梁。可見, ACI 規范公式計算結果偏于保守,但是對剪跨比大于3 的梁不夠安全。
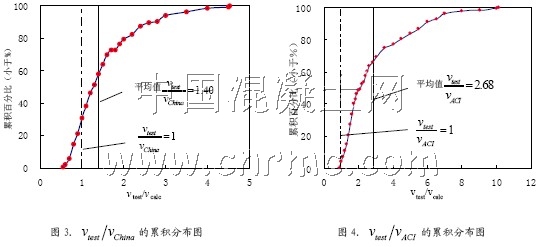
為了更直觀的體現試驗抗剪強度小于計算抗剪強度的梁所占的比例,做試驗值與計算結果比值的累積布圖于圖3和圖4。圖3顯示,試驗值與中國規范計算結果比值vtest/vChina小于其平均值1.40 的數據占總數據的58%,vtest/vChina<1的數據占總數據的31%。圖4 表明,試驗值與ACI 規范計算結果比值vtest/vACI小于其均值2.68 的數據占總數據的68%,vtest/vACI<1的數據占總數據的4%。
4 無腹筋梁抗剪承載力影響因素
影響梁抗剪承載力的主要因素為混凝土強度、剪跨比、截面有效高度和縱筋配筋率。下面將所收集到的國內外研究者的試驗數據分別按以上幾種因素進行分析。
4.1 混凝土強度等級
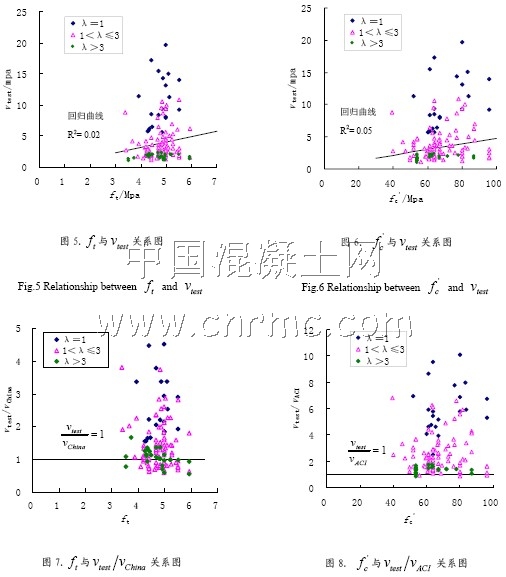
無腹筋混凝土梁的剪切破壞最終由混凝土材料的破壞控制,所以其剪切承載力隨混凝土的強度而提高。不同剪跨比的梁,因其破壞形態的差別,承載力分別取決于混凝土的抗壓和抗拉強度。中國規范用的是混凝土抗拉強度ft,美國規范用的是混凝土圓柱體抗壓強度fc。在圖5和圖6中分別給出混凝土抗拉強度ft和抗壓強度fc與梁抗剪強度試驗值vtest 的關系圖,圖中可見,vtest與ft和fc有大致的線性關系,但是數據的離散性很大,回歸曲線的相關系數都很低。圖7 給出了抗剪強度試驗值與中國規范計算值比值vtest/vChina與混凝土抗拉強度ft之間的關系圖。圖中可以看出,隨著ft的增加,vtest/vChina<1的點越多,說明混凝土強度越高,中國規范計算的抗剪強度安全度越低。從圖中還可以看出vtest/vChina<1的點多為剪跨比λ>3的梁,可見中國規范對于大剪跨比的高強混凝土梁不夠安全。圖8 為抗剪強度試驗值與美國規范計算值比值vtest/vACI與混凝土抗壓強度fc之間的關系圖,圖中幾乎所有的點都在vtest/vACI=1以上,可見美國規范用于高強混凝土無腹筋梁抗剪強度計算是安全的。
4.2 剪跨比
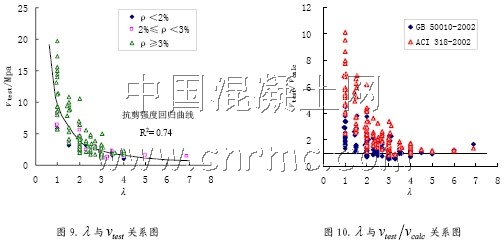
梁的剪跨比反映了梁的剪切破壞形態,是梁抗剪強度的主要影響因素。圖9 給出了梁的剪跨比與抗剪強度試驗值之間的關系,可以看出,剪跨比與抗剪強度的相關性較好。當剪跨比由小增大時,在λ<2 區間,抗剪強度下降很快;2≤λ≤3區間,抗剪強度的變化已經很小。λ>3以后,剪跨比對梁的抗剪強度影響不大。這主要是因為梁在抗剪過程中同時存在“梁作用”和“拱作用”λ<3時“拱作用”較大,而λ>3以后“拱作用”逐漸減弱造成的。圖10 為剪跨比與抗剪強度試驗值與計算值的比值test calc v v 的關系圖,圖中給出了試驗值與中國規范計算值的比值點和試驗值與美國規范計算值的比值點。可見在剪跨比λ < 2 時,兩國規范數據點均在vtest/vcalc=1以上,說明兩國規范公式在此區間都是安全的,但是美國規范比中國規范要保守;而當λ≥2 時,中國規范有相當一部分點落在了vtest/vcalc=1以下,說明中國規范公式對于大剪跨比的梁不安全;美國規范當λ>3時也不安全。
4.3 梁的尺寸效應
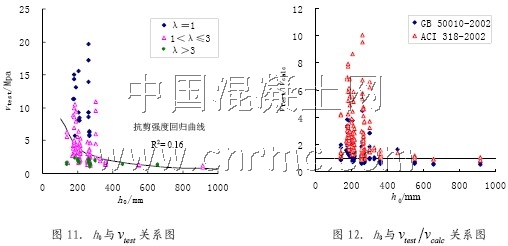
試驗數據分析表明,無腹筋梁的抗剪強度受尺寸效應的影響。即在混凝土強度、縱筋配筋率和剪跨比一定的情況下,隨著梁的有效截面高度增加,抗剪承載力呈下降趨勢,如圖11 所示。尺寸效應的原因可以解釋為,隨著截面高度的增加,在斜裂縫的寬度增大,骨料之間的咬合作用削弱,導致承載能力下降。圖11 還表明尺寸效應的大小與剪跨比密切相關,對于λ>3的梁,有效高度對抗剪強度幾乎沒有影響。
圖12 為試驗值與計算值隨梁截面高度變化的關系圖,圖中可以看出當梁截面有效高度大于200mm時,有不少中國規范計算值小于試驗值,而我國規范規定的截面高度影響系數的起點是800mm,相對來說安全性不足。美國規范也有少數點落在了vtest/vcalc=1一下,說明其對尺寸效應的考慮也不充分。Kim[8]的試驗也得到同樣的結果,并且證明ACI 規范公式用于d=915mm 的高強混凝土無腹筋梁的抗剪強度計算是不安全。
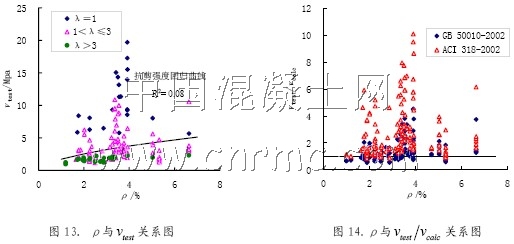
4.4 縱筋配筋率
縱向鋼筋除了直接提供銷栓力以外,還使梁的中和軸降低,從而加大了斜裂縫頂部混凝土受壓區高度,間接提高梁的抗剪承載力。圖13 給出了縱筋與抗剪強度之間的關系,可見隨著縱筋配筋率的增加,梁的抗剪強度增大,但是數據離散性很大,縱筋配筋率與梁的抗剪強度的相關性較差。圖中還顯示對于小剪跨比的梁,縱筋配筋率對抗剪強度影響較大,但是當剪跨比λ > 3時,增大縱筋率對梁的抗剪承載力幾乎沒有影響。圖14 則表明了梁抗剪強度試驗值與計算值的比值隨縱筋配筋率之間的關系,圖中無論是用中國規范還是用ACI 規范計算,均有部分數據點落在了vtest/vcalc=1以下,
可見兩國規范都沒有合理考慮這一影響因素,中國規范相對ACI 規范可靠性更低。
5 結論
本文收集國內外學者關于集中荷載作用下的高強混凝土無腹筋梁抗剪試驗數據158個,將試驗結果分別與中國規范GB50010-2002、美國規范ACI 318-2002提供的抗剪強度計算公式計算結果進行分析比較,得出以下結論:
(1)中國規范抗剪公式對于小剪跨比的梁偏于保守,對大剪跨比的梁不夠安全,沒有合理考慮尺寸效應和縱筋配筋率對梁抗剪承載力的影響,總體可靠度偏低。
(2)美國規范抗剪公式高估了混凝土抗壓強度的影響,低估甚至忽視了剪跨比、尺寸效應和縱筋配筋率對梁抗剪承載力的影響,對于剪跨比大于3 的梁不安全,總體可靠度較高,并且偏于保守。
參考文獻:
[1] 陳肇元,朱金拴,吳佩剛.高強混凝土及其應用[M].北京:清華大學出版社,1992.
[2] 施嵐清. 混凝土強度(140#~1100#)對無腹筋梁抗剪強度影響的試驗研究[R]. 清華大學土木系,海后設計局.1981,3
[3] Andew.G.Mphorde and Gregory. C. Frantz. Shear test of high-and low-strength concrete beams without stirrups[J]. ACI Journal, 1984,81(4):350-357
[4] Shuaib H. Ahmad,A.R.Khaloo,A. Poveda. Shear Capacity of Reinforced High-strength Concrete Beams[J]. ACI Journal,1986,83(2):197-305
[5] Ashraf H. Elzanaty,Arthur H. Nilson,Floydo. Slate. Shear Capacity of
Reinforced Concrete Beams Using High Strength Concrete[J]. ACI Journal, 1986,83(2):296-298
[6] Mark K. Johnson and Julio A. Ramirez. Minimum Shear Reinforcement in
Beams With Higher Strength Concrete[J]. ACI Structural Journal, 1988,86(4):376-382
[7] 趙光儀,吳佩剛,趙成文等.高強混凝土受彎構件的抗剪強度[J].土木工程學報,1991,24(2):10-18
[8] Jin-Keun Kim, Yon-Dong Park. Shear strength of reinforced high strength
concrete beams without web reinforcement[J]. Magazine of Concrete Research,
1994,46(166):7-16
[9] YoungSoo Yoon,William D.Cook, Denis Mitchell. Minimum Shear
Reinforcement in Normal, Medium, and High-Strength Concrete Beams[J]. ACI
Structural Journal, 1996,93(5):576-584
[10] Sung-Woo Shin, Kwang-Soo Lee, JungIll Moon, S.K.Ghosh. Shear Strength
of Reinforced High-Strength Concrete Beams with Shear Span-to-Depth Ratios between 1.5 and 2.5[J]. ACI Structural Journal, 1999,96(4):549-556
[11] Raghu S. Pendyala, Priyan Mendis. Experimental Study on Shear
Strength of High-Strength Concrete Beams[J].ACI Structural Journal, 2000,97(4):564-571
[12] F. J. Vecchio, W. Shim. Experimentral and Analytical Reexamination
of Classic Concrete Beam Tests[J]. Journal of Structural Engineering, ASCE,
2004,130(3):460-469
[13] 支運芳等.集中荷載作用下超高強混凝土無腹筋梁抗剪強度的試驗研究[J].重慶工學院學報,2005,19(3):69-75
[14] A. Cladera, A. R. Mari. Experimental Study on High Strength Concrete
Beams Failing in Shear[J]. Engineering Structures, 2005,27:1519-1 527
[15] Ahmed K, El-Sayed, Ehab F.ElSalakawy, Brahim Benmokane. Shear
Capacity of High-Strength Concrete Beams Reinforcement with FPP
Bars[J]. ACI Structural Journal, 2006,103(3):383-389

















