摘要:當橋面水泥混凝土出現裂縫時,針對垂直荷載作用下的防水層在裂縫上產生的變形,建立了計算防水層延伸率和抗拉強度的模型,可以有效計算出在此工況下防水層須具備的最小延伸率和拉伸強度。計算表明,延伸率低的防水層,要求有高的抗拉能力,而在裂縫寬度一定時,變形能力大的防水層適應能力強。利用有限元法分別對直接加鋪瀝青混凝土和設防水層的兩種橋面鋪裝結構進行實體建模,研究了在行車荷載作用下,當瀝青混凝土面層出現開裂時,橋面各鋪裝層的模量、厚度對鋪裝層層間法向拉應力的影響。結果表明,對直接加鋪瀝青混凝土面層的鋪裝結構,瀝青面層厚度在一定范圍內變化可以使鋪裝結構具有較好的受力性能,對于設防水層的橋面鋪裝結構,防水層模量是影響層間法向拉應力的主要因素。
關鍵詞:道路工程;混凝土橋面;瀝青混凝土;防水層;拉應力;模量
0 引言
據文獻[1]表明,在自身應力和荷載作用下,橋面水泥混凝土通常會產生裂縫;而在橋梁負彎矩區瀝青混凝土鋪裝層常出現裂縫損壞,面層剝落往往在裂縫處表現得更加明顯。本文針對在橋面水泥混凝土出現裂縫時,通過分析垂直荷載作用下的防水層實際變形,建立防水層張力計算模型,研究橋面防水層須具備的延伸率和拉伸強度;利用有限元法對直接加鋪瀝青混凝土和鋪設防水層的兩種橋面鋪裝結構進行實體建模,研究在行車荷載作用下,當瀝青混凝土面層出現開裂時,橋面各鋪裝層的模量、厚度對鋪裝層層間法向拉應力的影響。
1 橋面水泥混凝土裂縫處防水層抗拉分析
在橋面水泥混凝土裂縫處,防水層受均勻豎向荷載作用時,呈現弧形下陷。其下陷變形曲線呈圓弧形,同時因延伸而產生張力(每單位寬度的力,N/m)。如圖1所示,張力方向沿圓弧的切線方向。其方程如下:

式中:b為縫隙寬度;r、α、y意義如圖1中所示。

在平面應變條件下,防水層所受張力可簡化如圖2所示。取縫隙上防水層為隔離體(縱向取單位長度),則

則 T=p·b·f(ε) (4)
式中:T——縫隙上防水層所受的張力(N/m);
p——作用于防水層上的壓力,標準軸載作用于面層時,輪壓q=0.7MPa,傳遞到防水層時隨路面厚度h增大而減小,為安全起見,取p=q=0.7MPa;
ε——防水層的延伸率;
f(ε)——因防水層延伸率而異的計算因子(無量綱)
根據延伸率ε的定義有:

由(5)、(6)式可知,f(ε)隨ε呈一定規律變化。一般情況下多為前一種情形,即(5)式。考慮到計算模型的假設條件、荷載重復性、應力集中和其他自然因素的影響,將公式(4)乘以安全系數Ks得:
T=Ks·p·b·f(ε) (7)
Ks一般取3.0
混凝土內的裂縫一般不超過2mm,對于延伸率為30%的防水材料,利用公式(7)可以計算出由于裂縫而導致的張力T`≈2.1×103(N/m),換算為拉伸強度為105N/cm2。
從上述公式分析可得,對延伸率低的防水層,要求有高的抗拉能力,但并不是防水層的抗拉強度高就能防裂。在基層裂縫寬度一定時,變形能力大的防水材料適應能力強。結合文獻[2]的研究成果,與橋面混凝土一定寬度裂縫上防水層須具備的拉伸強度相疊加,則可得出防水層必須滿足的最小拉伸強度。
2 不設防水層的橋面鋪裝結構層間法向拉應力分析
2.1 基本假定
(1)橋梁梁體和水泥混凝土調平層為一剛性體;(2)各層材料具有線彈性性質,用E表征;(3)橋面鋪裝層層間完全連續接觸;(4)瀝青混凝土鋪裝層處于開裂狀態;(5)忽略橋梁震動對計算的影響。
2.2 計算模型、荷載最不利位置及基本參數
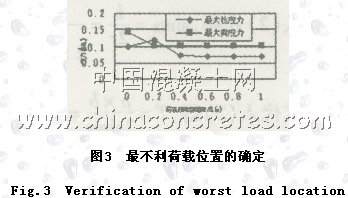
采用ANSYS有限元軟件進行空間實體建模,用空間八節點單元模擬。邊界條件為橋面板底面固定約束,四周為側向約束,面層自由裂縫對應一側有側向約束。荷載大小為BZZ-100,單元荷載為25KN,標準荷載圓半徑10.65cm。基本計算參數見表1。當荷載位置在裂縫邊緣處,水泥混凝土模型為8×4×0.35(m)時,拉應力均收斂,故基本模型采用8×4×0.35(m)。瀝青面層和橋面板的網格密度為20×20×10(cm)、20×20×25(cm)。確定模型的基本尺寸后,計算結果(圖3)表明,荷載圓距離裂縫20cm處是荷載最不利位置,最大法向拉應力出現在裂縫邊緣處。

2.3 瀝青混凝土面層和橋面板水泥混凝土模量的影響
分析表2和表3中計算結果可知,瀝青混凝土模量(Ea)瀝青混凝土面層和橋面板水泥混凝土模量(Ec)對層間拉應力影響很小,可以不予考慮。

2.4 瀝青混凝土面層和橋面板水泥混凝土厚度的影響
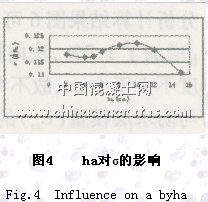
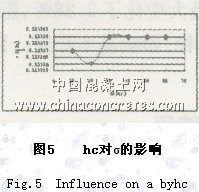
分析計算結果圖4、圖5知,瀝青混凝土面層厚度(ha)在2cm—4cm、4cm—10cm、10cm—15cm三個變化范圍內,層間拉應力經歷了先下降后上升,然后在面層厚度10cm處迅速下降的過程。層間拉應力變化百分比分別為1.14%、4.79%、9.28%。而橋面板水泥混凝土厚度(hc)變化對層間拉應力的最大改變僅0.017%,可不予考慮。因此可以認為,在考慮層間剪應力變化規律的情況下,面層厚度在一定范圍內變化可以使鋪裝結構具有較好的受力性能。
3 設防水層的橋面鋪裝結構層間法向拉應力分析
基本假設、計算模型與基本參數見2.1和2.2節,其中防水層的基本計算參數Em=150MPa、hm=3mm。確定荷載最不利位置為荷載圓距離裂縫20cm處,最大法向拉應力出現在裂縫邊緣處。
3.1 瀝青面層和水泥混凝土調平層模量的影響
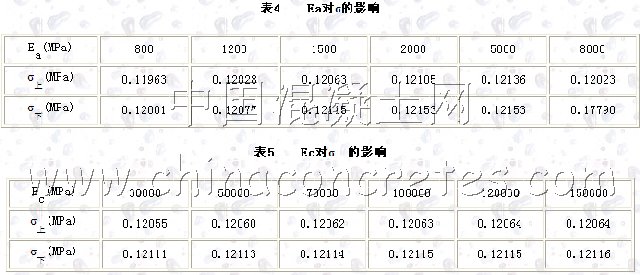
計算表4結果顯示,瀝青混凝土模量(Ea)從800MPa增長到8000 MPa,防水層與瀝青鋪筑層之間的法向拉應力(以下簡稱σ上)值最大變化了1.45%,防水層與橋面板之間的法向拉應力(以下簡稱σ下)值最大變化了1.27%。由表5知,橋面板水泥混凝土調平層模量(Ec)從30000 MPa變化到1500000 MPa,法向拉應力σ上最大變化了0.07%,法向拉應力σ下最大變化了0.04%。因此,可以忽略瀝青混凝土模量和橋面板水泥混凝土調平層模量對層間法向拉應力的影響。
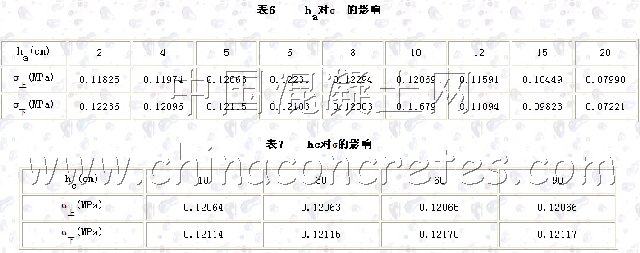
3.2 瀝青面層和水泥混凝土調平層厚度的影響
分析計算表6結果知,瀝青混凝土厚度(ha)由2cm增加到8cm的過程中,法向拉應力σ上最大變化了3.94%;法向拉應力σ下最大變化了1.59%,影響微小。瀝青混凝土厚度由8cm增加到20cm時,σ上減小了35.01%,σ下減小了39.84%。由于瀝青混凝土面層厚度一般不大于10cm,故可以不考慮瀝青面層厚度變化對層間拉應力的影響。由表7知,橋面水泥混凝土調平層厚度(hc)在10cm至90cm之間變化時,法向拉應力σ上最大變化了0.02%;法向拉應力σ下最大變化了0.46%,因此,不考慮調平層厚度變化對層間拉應力的影響。
3.3 防水層厚度及模量的影響
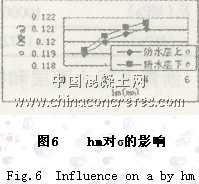
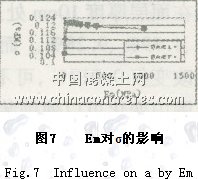
分析計算結果圖6可知,防水層厚度(hm)由1mm增加到4mm,法向拉應力σ上增加了1.7%,法向拉應力σ下增加了1.9%,影響甚微。由于一般防水層厚度不大于4mm,故不考慮防水層厚度變化對層間拉應力的影響。根據拉應力與防水層模量(Em)的變化規律,可根據Em將圖7中的曲線劃分為三個區段,即10~50MPa、50~300MPa、 300~1500MPa。當Em從10MPa增加到50MPa時,曲線變化速率最大,法向拉應力σ上增加了7.89%,法向拉應力σ下增加了16.15%;當Em從50MPa增加到300MPa時,σ上最大變化了1.71%,σ下最大變化了2.88%,影響較大;當Em在300~1500MPa區間時曲線變得更加平穩,影響基本穩定。因此,須考慮防水層模量變化對層間拉應力的影響。
3 結語
(1)針對防水層在橋面板裂縫處受豎向荷載作用的變形情況,建立了防水層張力的計算模型,可以有效計算出在橋面水泥混凝土一定寬度裂縫處,防水層必須具備的最小延伸率和拉伸強度。對延伸率低的防水層,要求具有高的抗拉能力;在橋面裂縫寬度一定時,變形能力大的防水層適應能力強。
(2)對于直接加鋪瀝青混凝土面層的鋪裝結構,若瀝青面層開裂,瀝青混凝土和橋面板混凝土的模量對層間法向拉應力影響不大;隨瀝青面層厚度的增加,層間法向拉應力先下降后上升,在面層厚度10cm處迅速下降,這反映了在考慮層間剪應力變化規律的情況下,面層厚度在一定范圍內變化可以使鋪裝結構具有較好的受力性能。
(3)對于設防水層的橋面鋪裝結構,在瀝青混凝土面層出現裂縫處,瀝青混凝土面層的模量和厚度、水泥混凝土調平層的模量和厚度、防水層厚度等參數的變化對瀝青面層裂縫處的層間法向拉應力影響很小;防水層模量變化對層間法向拉應力影響重大。
參考文獻
〔1〕 季節,徐世法,羅曉輝.橋面鋪裝病害調查及成因分析〔J〕.北京建筑工程學院學報,2000,16(3),33-39.
〔2〕 張占軍,王虎,胡長順,王秉綱.水泥混凝土橋面瀝青鋪裝及防水層荷載彎曲應力分析〔J〕.中國公路學報,2004,17(4),37-40.

















