摘要:鋼筋銹蝕后鋼筋與混凝土的粘結強度降低,導致鋼筋混凝土柱的力學性能的變化。本文利用APDL參數化設計語言編制的命令流,建立銹蝕鋼筋混凝土柱的有限元模型,施加低周反復荷載,獲得滯回曲線,分析鋼筋銹蝕后柱的滯回性能,與相應試驗結論吻合較好。
關鍵詞:鋼筋銹蝕,鋼筋混凝土柱,ANSYS
1. 引言
柱是鋼筋混凝土框架結構的主要受力構件,由于混凝土保護層碳化、鋼筋銹蝕、保護層開裂和鋼筋與混凝土之間的粘結滑移,柱的承載力性能下降在所難免。主要表現在三個方面[1]:一是鋼筋銹蝕引起鋼筋截面減小和強度降低;二是鋼筋銹蝕將產生體積膨脹,導致混凝土保護層沿筋開裂、甚至剝落,從而使混凝土截面產生損傷;三是鋼筋與混凝土之間的粘結性能退化。
強烈地震下結構進入彈塑性狀態,地震動輸入給結構的大部分能量將在滯回變形中耗散,滯回耗能是結構重要的抗震性能之一。對于銹蝕鋼筋混凝土柱的滯回性能,國內外學者也做了相應的試驗研究,得到了一些有益的結論[2,3,4,5]。由于鋼筋混凝土的損傷裂化速度慢,試驗試件無論采用快速碳化銹蝕試驗還是自然條件獲得,都受到諸多因素的制約。隨著計算機技術的大力發展,模擬也在土木工程中大量應用。商業通用程序ANSYS 是一個功能非常強大的有限元分析程序, 具有功能完備的前后處理器、強大的圖形處理能力和分析計算能力,在混凝土結構有限元分析中顯示出很大的實用性、方便性。本文將在鋼筋混凝土損傷劣化研究的基礎上,利用APDL參數化設計語言編制的命令流,建立銹蝕鋼筋混凝土柱的有限元模型,施加低周反復荷載,獲得滯回曲線,分析鋼筋銹蝕后柱滯回耗能的變化。
2. 有限元模型的建立
某鋼筋混凝土矩形截面框架柱,截面尺寸500×500mm2 。柱高為3600mm。縱向鋼筋為HRB335級12φ18 ,沿柱高度方向配置箍筋為HPB235級φ 8@200 ,且在柱底與柱端一米范圍內加密為間距100mm。混凝土強度為C30 級,保護層厚度25mm。
為簡化模型節約計算資源,又要保證模擬的準確性,特作以下幾點假設:混凝土碳化深度為保護層厚度,所以碳化對混凝土強度的影響不予考慮;柱箍筋銹蝕影響不予考慮,假定仍粘結良好,柱縱筋的銹蝕為均勻銹蝕,銹蝕率為7%。
2.1 單元類型的選取
為了更好的模擬鋼筋混凝土之間的粘結滑移特性,鋼筋混凝土柱采用分離式模型,選擇單元有:混凝土-solid65八節點六面體實體單元,鋼筋-link8桿單元,鋼筋和混凝土之間粘結作用-combin39彈簧單元。
混凝土材料的三維實體單元solid65,由八個節點組成,每個節點具有三個方向的自由度,solid65單元可以模擬混凝土材料開裂、壓碎、塑性變形和蠕變的特性。
鋼筋選取三維link8單元,該單元有兩個節點組成,具有三個方向的自由度。link8單元在工程分析上應用廣泛,可以用來模擬桁架、纜索、連桿、鋼筋等。這種三維桿單元是桿軸方向的拉壓單元,每個節點具有三個自由度,不承受彎矩,具有塑性、蠕變、膨脹、應力剛化、大變形、大應變等功能。
彈簧單元combin39是一個具有非線性功能的單向單元,本單元都有軸向或扭轉功能。軸向選項代表軸向拉壓單元,每個節點具有三個自由度即沿節點坐標系X、Y、Z 的平動,不考慮彎曲和扭轉;扭轉選項代表純扭單元,每個節點具有三個自由度即繞節點坐標軸X、Y、Z 的轉動,不考慮彎曲和軸向荷載。
2.2 材料本構關系模型的選取
在鋼筋混凝土有限元分析中,準確定義材料本構關系將對計算結果有著至關重要的意義。
在solid65單元中的材料屬性需通過定義兩個數據表:一個是本構關系的數據表,采用多線性等向強化(MISO)模型描述混凝土應力-應變關系;另一個用于定義混凝土的破壞準則,通過混凝土單元材料特性表定義混凝土的裂縫張開剪力傳遞系數、閉合剪力傳遞系數、單軸和多軸抗壓強度等9個參數, 定義混凝土的William-Warnke強度準則。本構關系選擇混凝土單軸向受壓應力應變曲線的E.Honested 建議的模型(公式1~2)。
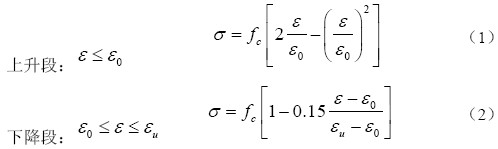
對于模擬鋼筋材料的link8單元,定義一個應力-應變關系的數據表,采用雙線性等向強化(BISO)模型描述混凝土和鋼筋的應力-應變關系。文獻[6]通過電化學銹蝕試驗并結合非線性有限元分析,給出了銹蝕鋼筋名義屈服強度和延伸率的變化規律,本文按其提出的計算公式(3~6)進行分析計算:


用combin39來模擬鋼筋和混凝土之間的粘結作用,彈簧性能由彈簧的力—位移(F-D)曲線確定,程序中用實常數20對數表示。
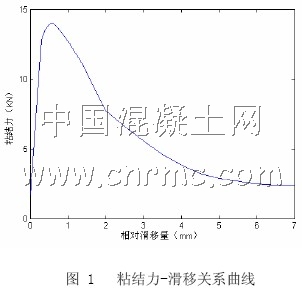
F-D曲線可以通過粘結滑移本構關系τ =τ (s),由以下公式確定,其數學表達式為:F =τ(D)× Ai其中, i A 為該彈簧所對應的在接觸面上所占的面積。參考文獻[7]通過對試驗數據的回歸分析,得到完好構件鋼筋混凝土的粘結滑移,再利用銹后鋼筋和混凝土粘結強度降低系數,得到本文銹蝕鋼筋混凝土柱的F-D曲線,如圖1所示。
2.3 建模及網格劃分
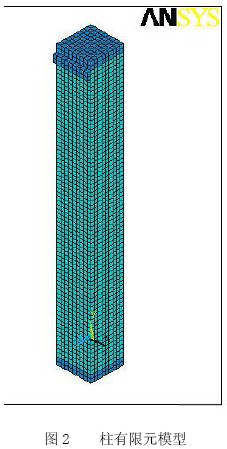
采用實體建模功能直接建模,采用分離模型考慮鋼筋和混凝土之間的滑移, 通過三個非線性彈簧單元,分別代表沿接觸面平行于縱向鋼筋和垂直于縱向鋼筋方向模擬鋼筋與混凝土間的相互作用,來實現位移協調。網格劃分為適當的密度有助于收斂,在建模過程中對單元尺寸進行有效控制,可以有效避免應力集中帶來的問題,在鋼筋混凝土模型的單元尺寸取5cm。鋼筋混凝土柱形狀很規則,采用映射方式單元劃分,混凝土單元是5832個Solid65 單元,鋼筋單元是1908個Link8 單元,鋼筋與混凝土的粘結單元是2592個combin39單元。網格劃分情況見圖2。
2.4 邊界約束和加載方式
為防止產生應力集中,在支座和集中力作用處加一個小尺寸的剛性墊塊,用Solid45單元來模擬,通過共用節點使剛性墊塊節點與相應的混凝土節點位移協調。柱底節點固結,并在柱頂設置定向支座。在柱頂施加豎向荷載,達到軸壓比為n=0.3,柱頂端側面施加單調位移荷載和低周反復荷載兩種工況,用位移的∞-范數控制收斂,誤差控制可以在2%~3%之間,合理設置子步數,打開線性搜索、預測等項以加速收斂,打開應力松弛開關,加速裂縫即將開裂時計算的收斂。
3. 有限元計算結果分析
3.1 單調加載工況
對有限元模型施加單調荷載:施加水平向 12mm 靜位移作用,計算完成后,進入ANSYS的時間歷程后處理界面,利用APDL參數化設計語言編制的命令流提取柱底剪力及柱頂位移值,即可得剪力與柱頂位移的關系曲線(如圖4所示)。
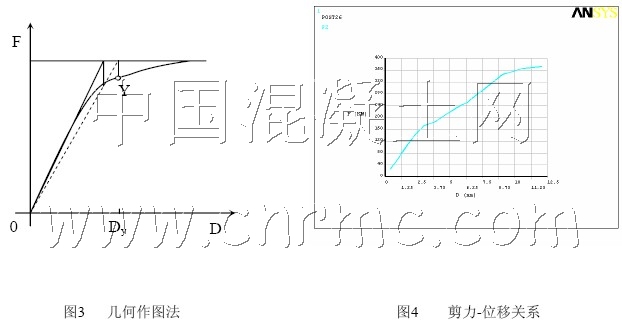
鋼筋混凝土柱的屈服點判斷是一個比較復雜的問題,國內外尚無統一標準。本文采用文獻[8]介紹的幾何作圖法(如圖3所示),Y點為確定的力-變形曲線上的屈服點,對應的Dy為屈服時的構件或結構初始屈服變形。采用此方法可在圖 上確定出該柱的初始屈服位移為7.8mm,依據此位移值,可確定鋼筋混凝土柱進行彈塑性有限元分析的起始位移可選為7.5mm。
3.2 低周反復荷載工況
對有限元模型施加反復荷載:施加水平向低周反復位移作用,依據單調加載結構的分析,
起始位移選為±7.5mm,逐級加載。計算完成后,進入ANSYS的時間歷程后處理界面,利用APDL參數化設計語言編制的命令流提取柱底剪力及柱頂位移值,即可得到該鋼筋混凝土柱的滯回曲線(如圖5所示)。
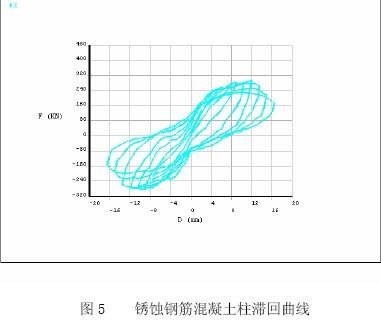
單軸受力構件在循環反復荷載作用下的力-變形曲線稱為構件的單軸滯回曲線,簡稱滯回曲線。在銹蝕鋼筋混凝土柱反復荷載作用的剪力位移圖,從圖上可以看出:
(1)鋼筋混凝土柱在開始進入屈服時,加載變形曲線的斜率變化小,卸載后的殘余變形也小,正反向加載各一次所構成的滯回環不顯,基本上重合為一條直線。
(2)在荷載繼續地反復作用,拉應變和壓應變不斷地積累增大,構件留有殘余變形,對粘結彈簧單元影響較大,總的變形持續地增加,而承載變化不大,變形曲線的斜率逐漸減小,這與反復加載下構件的剛度退化有關。
(3)數次反復加載之后,變形曲線上出現了較明顯的拐點,形成滯回曲線的捏攏現象,表明滯回耗能能力已經下降。
體系的滯回耗能等于往復循環過程中各滯回環包圍的面積之總和,是恢復力在滯回過程
中所耗散的能量。在鋼筋銹蝕的情況下,柱的耗能能力降低,抗震性能發生了退化。
4. 結論
利用 ANSYS 有限元軟件提供的實體單元SOLID65、桿單元LINK8、彈簧單元Combine39較好的建立了銹蝕混凝土柱的有限元模型,并通過單調加載和低周反復加載,得到了鋼筋銹蝕后混凝土柱的力學性能的變化,為進一步建立銹蝕鋼筋混凝土柱的恢復力模型提供依據。
本文很好的實現對鋼筋混凝土柱的滯回性能仿真分析,與同類型銹蝕構件的試驗相比較,也能夠取得較為理想的結果。
參考文獻
[1]牛荻濤.《混凝土結構耐久性與壽命預測》[M].北京:科學出版社,2003.2。
[2]Okada Kiyoshi,Kobayashi Kazuo, Miyagawa Toyoaki. Influence of longitudinal cracking due to reinforcement corrosion on characteristics of reinforced concrete members. ACI Structural Journal[J].134-140, March-April.1988
[3]顏桂云,孫炳楠,王澤軍等.銹蝕鋼筋混凝土壓彎構件抗震性能的試驗研究[J].建筑結構,2003,33(2):16-18。
[4]王學民.銹蝕鋼筋混凝土構件抗震性能試驗與恢復力模型研究[D].西安:西安建筑科技大學,2003。
[5]劉伯權,劉鳴.鋼筋混凝土柱的破壞與能量吸收[J].地震工程與工程振.1998,18(3):14-18。
[6]袁迎曙,余索.銹蝕鋼筋混凝土梁的結構性能退化[J].建筑結構學報.1997,18(4):51-57。
[7]徐善華.混凝土結構退化模型與耐久性評估[D].西安:西安建筑科技大學,2002。
[8]張新培.鋼筋混凝土抗震結構非線性分析[M]. 北京:科學出版社.2003.9。

















